Векторлорду кошуу
|
|
Жабдуулар:
- күч
столу;
-
кыскычтуу
чыгырыктар;
-
жүктөрдүн
тобу;
- транспортир,
сызгыч
Максат: Күч
столунун
жардамы
менен күч
векторлорунун
суммасын
табуу.
Алынган
натыйжаны
векторлорду
кошуунун
түзүүчүлөргө
ажыратуу
ыкмасы жана
геометриялык
ыкма аркылуу
текшерүү.
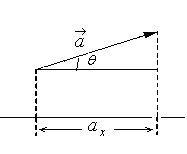
Күч. Күч вектору
|
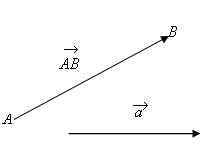
2.1- сүрөт.
Вектордун
сүрөттөлүшү |
Вектор деп
багытталган
кесинди
аталат.
Вектор үстүнө
жебе белгиси
сызылган бир
тамга же
вектордун
башын жана
учун
көрсөткөн
баш тамгалар
менен
белгиленет: 
, 
, 
ж.у.с. Бул
кесиндинин
узундугу вектордун абсолюттук
чоңдугу
же модулу
деп аталат да,
же 
түрүндө
белгиленет.
Кандайдыр
окко карата
вектордун
жайгашуу
бурчу вектордун
багыты
катары кабыл
алынат.
Бир түз
сызыкка
жарыш болгон
же бир түз
сызыкта жаткан
векторлор
коллинеардуу,
ал эми бир тегиздикке
жарыш болгон
векторлор
компланардуу
векторлор
деп аталат.
Физикалык
чоңдуктар
эки чоң топко,
атап
айтканда,
скалярдык
жана вектордук
чоңдуктарга
бөлүнүшөт.
Сан мааниси
боюнча
мүнөздөлүүчү
чоңдуктар скалярдык
чоңдуктар
деп аталат да,
аларды
кадимки
сандар менен
эле мүнөздөөгө
болот. Скалярдык
чоңдуктарга
мисал болуп
масса, температура,
узундук,
аянт, көлөм
эсептелет.
Сан мааниси
менен бирге
мейкиндиктеги
багыты менен
мүнөздөлүүчү
чоңдуктар вектордук
чоңдуктар
деп аталат.
Вектордук
чондуктарга
мисал катары
күч векторун
карап көрөлү.
Физикада күч
деп, нерселердин
өз ара
аракеттешүүсүнүн
чени аркылуу
аныкталуучу
физикалык чоңдукту
айтабыз. Бир
нерсенин
экинчи
нерсеге аракети
багыттуу
мүнөзгө ээ
болгондуктан,
күч вектордук
чоңдук болуп
эсептелет. Мисалы,
нерсеге 5
күч
аракет этсе,
анын кандай
багытта
аракет
эткендиги
көрсөтүлбөсө,
күч чоңдугу
толук берилди
деп айтууга
болбойт.
Күчтүн
аракети
менен нерсе
кыймылга
келиши же
деформацияланышы
мүмкүн.
Механиканын
динамика
бөлүмү күч
жана күчтүн
аракети
менен
байланышкан
кубулуштарды
ичине
камтыйт. Нерсеге
таасир эткен 
күчтөрүнүн
жалпы
аракети,
алардын вектордук
суммасына
барабар
болгон
натыйжалоочу
күчүнүн
таасирине
эквиваленттүү.
Динамиканын
негизи үч
закон
түрүндө Ньютон тарабынан
формулировкаланган.
Ньютондун биринчи
закону. Ар
кандай нерсе
өзүнүн тынч
абалын же бир
калыптагы
түз сызыктуу
кыймылын,
башка нерселер
тарабынан
өзгөртүүгө
аргасыз кылганга
чейин сактап
тура берет. Бул 
болгондо,
б.а.
нерсе тынч
абалда же бир
калыпта түз
сызыктуу кыймылда
болорун
билдирет.
Ньютондун
экинчи
закону. Күчтүн
аракети
менен нерсе
ээ болгон
ылдамдануу
ал күчтүн
чоңдугуна
түз жана
массасына
тескери
пропорциялуу
Мында күчү
жогоруда
белгиленгендей
натыйжолоочу
күч.
Ньютондун үчүнчү
закону. Аракетке дайыма барабар жана каршы
аракет
болот. Башкача
айтканда,
эки нерсенин
бир-бирине
кылган аракети барабар жана карама-каршы
багытталган
болот.
Биринчи нерсе
тарабынан
экинчи нерсеге аракет кылган күчтү 
, экинчи
нерсе тарабынан
биринчи нерсеге жасаган каршы аракетти
деп
белгилесек,
анда
жана 
күчтөрү
бир чекитке
эмес, эки
башка нерсеге
аракет кылгандыктан,
алардын
натыйжалоочусу
нөлгө барабар болбойт. Мында жана күчтөрү
бирин бири тең
салмактап
тургандыктан,
мындай күчтөр тең салмактоочу
күчтөр деп аталат.
Динамикада тең
салмактоочу
күч түшүнүгүнөн
сырткары
натыйжалоочу
күч түшүнүгү
колдонулат.
Тең салмактоочу
жана натыйжалоочу күч
деген түшүнүктөр
бирдей эмес.
Натыйжалоочу
күч – бул эки
күчтүн
суммасы
. Ал эми тең
салмактоочу 
күч
чоңдугу
боюнча
натыйжалоочу
күчкө
барабар,
бирок
карама-каршы
багытталат,
жана аны тең
салмактап
турат:
2.2 - сүрөт
Нерсеге аракет эткен күчтөрдү талдоодо векторлорду кошуунун ар түрдүү ыкмалары колдонулат. Биз төмөндө тажрыйбалык, геометриялык жана түзүүчүлөргө ажыратуу ыкмаларына токтолобуз.
Векторлорду кошуу
|
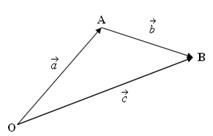
2.3 - сүрөт.
Векторлорду
үч
бурчтук
эрежеси
боюнча
кошуу |
Геометриялык
ыкма.
Берилген жана 
векторлорунун
суммасы
болгон
векторун
табуу
үчүн,
каалаган 
чекитин
алып, адегенде
векторун
түзүп, андан
кийин А
чекитинен 
векторун
ченеп коебуз.
Биринчи вектордун
башталышы
менен экинчи
вектордун учун
туташтырган 
вектору
берилген жана векторлорунун
суммасы деп
аталат да, 
деп
белгиленет. Векторлорду
кошуунун бул
ыкмасы
үч бурчтук
эрежеси деп
аталат (2.3-сүрөт).
|
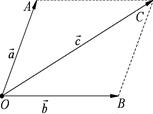
2.4 - сүрөт. Векторлорду
параллелограмм эрежеси
боюнча кошуу |
Эгер жана векторлору
коллиенардуу
болушпаса,
анда алардын
суммасы
параллелограмм
эрежеси боюнча да табылат.
Ал үчүн чекитинен жана
векторлорун
ченеп коюп, 
жана
кесиндилерин
параллелограммга
толуктасак,
параллелограммынын
диагоналы жана
векторлорунун
суммасы
болот, б.а (2.4- сүрөт).
|
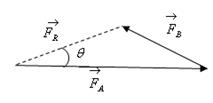
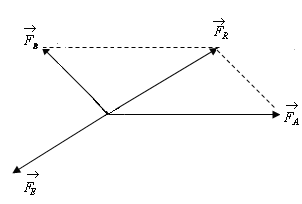
2.5-сүрөт |
жана векторлорунун
мисалында 
жана 
күч
векторлору
болгон болсо,
бул эки күч
сызгыч жана
транспортирдин
жардамы
менен
жогорудагы
эрежелерге
таянып
суммаланат. күчү күчүнүн
аягына
уланат.
Натыйжалоочу
күчү векторунун
аягы менен векторунун
учун
туташтыруучу
вектор болот
(2.5-сүрөт).
Вектордун
чоңдугун
сызгыч менен
өлчөп, ал эми
багытын ( θ
бурчун)
транспортирдин
жардамы менен
аныктоо
аркылуу 
тең
салмактоочу
күчүн
векторун
чийүүгө
болот.
|
2.6-сүрөт |
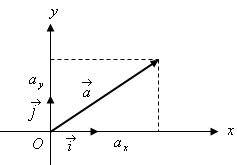
Түзүүчүлөргө
ажыратуу
ыкмасы. векторунун
огуна
болгон
проекциясы
деп 
кесиндисин
айтабыз (2.6-сүрөт), б.а. векторунун огуна
болгон проекциясы
скаляр жана
ал
болорун баамдоо
кыйын эмес.
Тегиздикте
координат башталышынан
чыккан векторунун
окторго болгон проекцияларын
,
аркылуу
белгилесек,
анда векторунун
бул
проекцияларын
деп
белгилеп
жазуу кабыл алынган.
Ох, Оу
окторунун
бирдик векторлорун 
, 
аркылуу
белгилеп,
векторлорунун
координаталары
боюнча ажыратылып
жазылышын
алабыз:
Мында
жана
векторунун
түзүүчүлөрү деп
аталат.
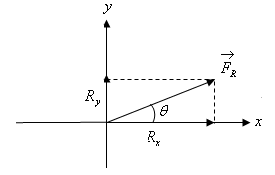
Вектордун
модулун, анын
окторго
болгон проекциялары
аркылуу
туюнтуп
алууга болот
(2.7-сүрөт),
б.а.
|
2.7-сүрөт |
Мында векторунун
проекциялары
, 
формулалары
менен
аныкталат. Вектордун модулу анын окторго
болгон проекцияларынын
квадраттарынын
суммасынан
алынган квадраттык
тамырга барабар.
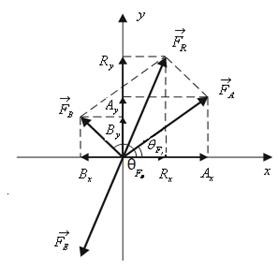
Эки
күчтүн натыйжалоочусун
алардын түзүүчүлөрү
аркылуу таба
алабыз. жана векторлорун
XY
координат
системасына
жайгаштырып,
түзүүчүлөргө
ажыратабыз
(2.8-сүрөт):
|
2.8-сүрөт |
жана
күчтөрүнүн
суммасын
табуу үчүн:
Мында 
-
натыйжалоочу
күчтүн
проекцияларын
туюнтушат.
Натыйжалоочу
күчтүн
чоңдугун
табуу үчүн
Пифагордун
теоремасын
колдонобуз: 
ал эми
багыты б.а. огуна
карата
жантаюу
бурчу
тригонометриялык
формула
менен
аныкталат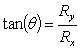 
.
2.9-сүрөттө
ыңгайлуу
болуш үчүн вектору
X огун
бойлото
жайгаштырылган,
демек, анын Y огуна
проекциясы
нөл болорун (
) эстен
чыгарбоо
керек.
|
|
|
2.9
- сүрөт
Натыйжалоочу
күч
табылгандан
кийин, тең салмактоочу
күчтүн
проекциялары -
жана -
болорун
түшүнүү
кыйын эмес.
Демек, ушул
проекциялар
менен тең
салмактоочу
күчтүн векторун
чийип алууга
болот.